De l'utilité des mathématiques

Le but de cette section n'est pas de faire oeuvre encyclopédique, mais après réflexion, je m'aperçois qu'un certain nombre de connaissances mathématiques sont nécessaires pour appréhender les techniques et les savoir-faire les plus rentables de l'industrie moderne. Ces mathématiques appliquées m'ont été source de soucis durant mes études, quoique passionnantes du reste; j'imagine qu'elles ont également été source de stress pour d'autres.

Imaginez donc un pays où il n'y aurait pas de diplômes, où les gens ne gagneraient leur vie que grâce à ce qu'ils savent faire et qu'ils montreraient. Le matheux aurait ainsi sa petite affaire et ses clients, à qui il proposerait de mettre en oeuvre ses connaissances pour résoudre des problèmes d'ordre intellectuel :

Gestion industrielle
Finances
Economie
Etude des rapports humains
Linguistique
Gestion documentaire
Etc...

L'expérience aidant, il affronterait des problèmes de plus en plus complexes, et aurait donc besoin d'outils mathématiques de plus en plus puissants et précis. Il irait donc apprendre sur le tas de nouvelles techniques et de nouvelles théories...Le cursus d'apprentissage serait radicalement différent de celui que nous avons pu connaître en université ou au lycée...Pas d'examen, pas de contrôle, pas de programme, tout le temps nécessaire pour prendre des notes et dessiner les concepts et les expérimenter sur ordinateur, le rêve !

Je me suis par ailleurs laissé dire que les golden boys les plus riches de la planètes étaient tous des cracks en mathématiques : A l'origine, les chiffres servent à dresser les comptes...
Maintenant, il m'est arrivé quelques fois de paniquer devant l'aridité d'un problème de mathématiques, mais surtout de devoir m'en justifier devant mon entourage : N'aurais-je pas mieux à faire à mon âge que d'étudier la topologie algébrique, la géométrie symplectique, bref de faire des maths ? Et puis, à quoi ça sert tout ça ? Un jour ou l'autre, il faut se poser la question, mais la réponse existe déjà : Deux disciplines sont viscéralement liées aux mathématiques, puisqu'elles en sont les génitrices dans l'histoire humaine :

L'économie et les affaires de finance
La géographie et les sciences de la Terre

La raison est très simple : pour l'économie, ce sont les affaires commerciales qui ont nécessité la mise au point des chiffres et des opérations arithmétiques. Aujourd'hui, ce sont les sphères de la finance qui sont de loin les plus consommatrices de modèles mathématiques, au point qu'il en existe une industrie intellectuelle appelée "quantitative analysis" chez les anglosaxons. Les matheux y sont surnommés les "quantsters"...Un des plus gros sites se trouve à "Analytic Bridge". Jérôme Kerviel aurait-il oublié de se servir de tels modèles pour observer et prévenir le risque ?
Pour la géographie, la raison est étymologique : la géométrie, la géodésie contiennent le lexème "géo-" qui vient du grec "Gê" et de l'égyptien "Geb", la Terre. Cadastres et arpentages sont les ancêtres de la topologie dont je parlais plus haut, et je dirais que la loi de l'univers intellectuel est une loi géographique, où l'on positionne des concepts les uns plus ou moins proches des autres comme on positionne des villes sur une carte.

Accès à la rubrique "mathématiques" du blog "SLCV"

Prendre conscience de sa mémoire déductive

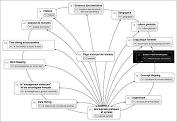
Je me souviendrai toujours de l'un de mes professeurs de mathématiques qui nous apprenait trois choses :

Dessinez, encore, encore et toujours, à outrance ! Vous ne devriez pas écrire vos cours, mais les dessiner. Vous devriez avoir le réflexe conditionné du dessin, même pour une simple phrase (sujet-verbe-complément) qui pose le problème...Plus tard, j'ai compris l'intérêt du dessin d'art et du mind-mapping
Les mathématiques ne s'apprennent pas comme l'histoire, elles font appel à la mémoire déductive
Enseignez comme vous auriez aimé que l'on vous enseigne..."fichez" par terre le cours, et remettez tout en question pour reconstruire patiemment. Cela pourrait ressembler à du Bouddhisme !

Concernant la mémoire déductive, le principe d'apprentissage est simple mais très peu connu. Sachez que je l'ai utilisé de manière assez spectaculaire pour réussir mes études scientifiques; si seulement vous pouviez l'essayez ne serait-ce qu'une seule fois !
Vous rentrez chez vous le soir, et vous venez d'avoir un cours de sciences, qu'elles soient dures ou molles, ça vous regarde !! (LoL)

Commencez par prendre une feuille blanche, à peu près dans le même genre que celle ci-dessous :

Puis essayez de vous rappeler de ce par quoi vous avez commencé le cours de science. Je dis bien ce par quoi vous avez commencé. Si des souvenirs vous viennent concernant le déroulement du cours, sachez qu'ils n'ont aucune valeur...
Si vous ne vous souvenez pas du début du cours, alors deux solutions :

Soit vous êtes arrivé en retard : Hé bin, c'est du joli !!
Soit vous n'avez pas compris l'intérêt même du cours, ni où le professeur voulait en venir. Cela arrive malheureusement souvent dans un enseignement théorique, où des connaissances auxiliaires sont exposées AVANT le vif du sujet, ce qui ne facilite pas l'attention et la concentration.

Puis, à partir du début du cours, essayez de vous souvenir de ce qui a été dit juste après, puis juste après, ainsi de suite...Vous avez un horrible trou de mémoire ? Hé bien, c'est précisément à cet endroit, à la ligne près, que vous n'avez rien compris à ce que le professeur a dit. C'est pour ainsi dire mathématique : la mémoire déductive est liée à la capacité d'enchaîner les concepts. Si donc vous ne vous en souvenez pas, de ce fichu paragraphe, c'est que votre cerveau n'a pas su le relier logiquement au paragraphe qui précède et à celui qui suit. La chaîne de compréhension est rompue à cet endroit précis. Il vous importe donc absolument de vous documenter sur des supports extérieurs, de vous faire aider par une autre personne sur ce point précis.

La désopilante naissance du calcul des probabilités

L'histoire des mathématiques est souvent amusante. L'exemple que je préfère est l'invention du calcul des probabilités. C'est l'histoire d'un savant, dont j'ai oublié le nom (ce qui ne peut que faire du bien à son Ego), et qui avait la sale manie d'aller jouer ses sous au casino. Lassé de se faire peler comme un mouton face à des habitués narquois et probablement peu honnêtes, il rentra chez lui pour écrire quelques équations afin de représenter la situation. Le but était d'estimer une fraction, nombre de cas favorables à un événement par rapport au nombre de cas possibles. Le calcul des probabilités était né...
Quelques siècles plus tard, le calcul des probabilités s'est tellement sophistiqué qu'il fait des ravages dans le porte-monnaie du patron de casino. Les agents de casino surveillent les comportements des joueurs pour voir s'ils ne seraient pas en train de s'en servir (comptage des cartes, martingale, répartition des risques par association de joueurs, etc...), auquel cas lesdits joueurs sont expulsés manu militari

Je vous souhaite donc de vous amuser à faire des maths, vous ne devriez pas y perdre trop d'argent et cela vous aidera certainement à digérer les autres pages de l'anneau de science...

Le vif du sujet

Analyse

dérivées, dérivées partielles, opérateurs vectoriels (gradient, divergence, rotationnel), le NABLA.
intégrale Riemann sous la courbe, lien vers pb plus complexes : intégrale & convergence, Lebesgue, distributions
nombres complexes et transformée de Fourier.
fractals ? intéressant, images et algorithmes.

Algèbres

Algèbres avec un "s".
calcul polynômial : les polynômes sont une algèbre, polynômes interpolateurs, développements finis, division entière entre polynômes, relation entre un réseau de neurones et une suite polynômiale.
Calcul matriciel : voir commentaires dans le code source pour la rédaction du contenu
algèbre linéaire jusqu'aux espaces euclidiens, lien vers analyse de données.
théorie des graphes, lien vers concept mapping.

Stats et probas

statistiques (descriptive, inférentielle)
probabilités (jusqu'à la ddp, reconnaissance de formes)
Description de lois de probas intéressantes :

Loi uniforme
Loi binômiale
Loi géométrique de Bernoulli
Loi de poisson
Loi de Gauss
Loi log-normale

des probas aux statistiques.
des statistiques aux probas.

Mélange des genres

outils pour faire des maths : les CAS, le principe du calcul symbolique, liens vers Scilab. géométrie dans l'espace : Voir commentaires dans le code source pour la rédaction du contenu
géométrie dans l'espace : orientation, hyperplan, extrusion, rotation, gemmes, quadriques

Sommaire